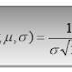Assalamualaikum wr. wb.
Halo teman teman semua, gimana kabar nya ? hehehe
Seperti biasanya, pada kesempatan kali ini kita akan membahas secara singkat tentang Uji Chi Squared.
Uji Chi Squared
Uji ini dapat digunakan untuk menyelesaikan berbagai masalah
1. Distribusi Sampling Variansi
2. Estimasi Variansi
3. Uji Hipotesis Propori dan variansi
4. Uji Kebaikan Suai
5. Uji Kebebasan
Uji Chi Squared : Pengujian Hipotesis perbandingan antara frekuensi observasi (aktual) dengan frekuensi harapan (ekspektasi).
Nilai Frekuensi Observasi : Hasil Percobaan
Nilai Frekuensi Harapan : Hasil Percobaan Secara Teoritis
Rumus :

Tabel Chi Squared

Oke, Selanjutnya ane mau kasih lihat video pembahsan tentang uji Chi Squared yang ane ambil dari Om YouTube hehe, Mudah mudahan denan video ini temen temen lebih mudah memahaminya, hehe
Oke mantapzz, Mungkin sekian dulu dari ane, jika ada pertanyaan silahkan tinggalkan pada kolom komentar ya,
Terima Kasih :)
Halo teman teman semua, gimana kabar nya ? hehehe
Seperti biasanya, pada kesempatan kali ini kita akan membahas secara singkat tentang Uji Chi Squared.
Uji Chi Squared
Uji ini dapat digunakan untuk menyelesaikan berbagai masalah
1. Distribusi Sampling Variansi
2. Estimasi Variansi
3. Uji Hipotesis Propori dan variansi
4. Uji Kebaikan Suai
5. Uji Kebebasan
Uji Chi Squared : Pengujian Hipotesis perbandingan antara frekuensi observasi (aktual) dengan frekuensi harapan (ekspektasi).
Nilai Frekuensi Observasi : Hasil Percobaan
Nilai Frekuensi Harapan : Hasil Percobaan Secara Teoritis
Rumus :
Tabel Chi Squared

Oke, Selanjutnya ane mau kasih lihat video pembahsan tentang uji Chi Squared yang ane ambil dari Om YouTube hehe, Mudah mudahan denan video ini temen temen lebih mudah memahaminya, hehe